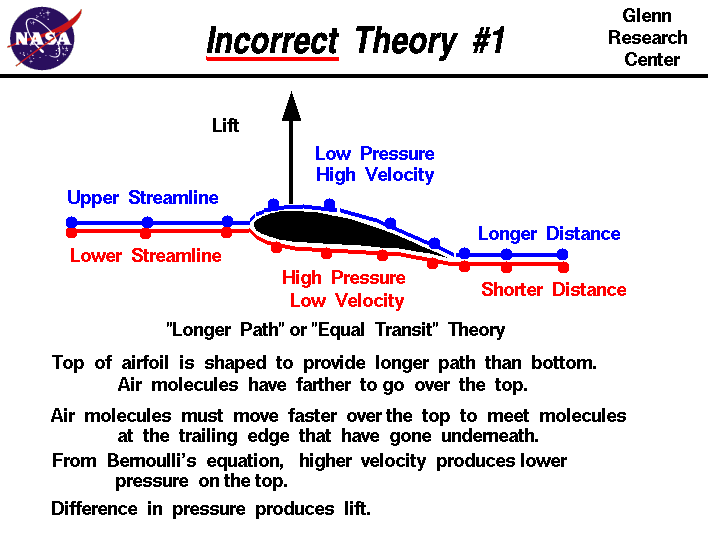
EQUAL TRANSIT TIME THEORY – APAKAH INI BENAR?

Berbagai macam sumber telah berusaha menjelaskan bagaimana lift dapat dihasilkan. Salah satu teori yang paling popular adalah teori equal transit time. Teori ini begitu popular dalam literature modern, mulai dari ensiklopedia sampai ke beberapa textbook.1 Ketika saya masih SMA dulu, saya juga diajarkan mengenai teori ini untuk menghitung gaya angkat pesawat. Tetapi apakah teori ini benar?

Di referensi [1], anda dapat menemukan Java Applet Simulation yang dapat menggambarkan lebih jelas mengenai kesalahan dari teori ini. Pembaca disarankan untuk mengunjungi NASA Glenn Website di [1] untuk informasi lebih jauh.

Teori ini mengatakan bahwa (1) airfoil pesawat di-design sedemikian agar panjang lintasan permukaan atas sayap lebih panjang daripada permukaan bawah sayap. Artinya (2) molekul udara di sisi atas sayap harus bergerak lebih cepat daripada molekul di sisi bawah sayap agar mereka bertemu lagi di ujung trailing edge sayap. (3) Karena aliran udara di atas sayap lebih cepat, maka berdasarkan Hukum Bernoulli (lihat persamaan di bawah ini), tekanan udara di atas sayap lebih rendah daripada di bawah sayap. (4) Perbedaan tekanan ini menghasilkan lift.

Pertama, mari kita lihat apa itu Hukum Bernoulli.

Daniel Bernoulli (1700-1782)

Hukum Bernoulli untuk suatu aliran pada ketinggian yang sama (artinya aliran tersebut tidak mengalir ke tempat yang lebih rendah/tinggi secara signifikan) dapat ditulis secara matematis sebagai berikut:

Dapat diartikan secara gamblang sebagai berikut. Apabila aliran udara mengalami perubahan kecepatan, tekanan udara di aliran tersebut juga berubah. Misalnya ada dua titik A dan B seperti di gambar berikut.

Titik A memilik kecepatan yang lebih tinggi daripada titik B karena titik A memiliki luas penampang yang lebih kecil daripada titik B. Coba bayangkan ketika anda menutup selang air sebagian, airnya memancar lebih kencang, bukan? Hukum Bernoulli menjelaskan bahwa perbedaan tekanan udara antara permukaan atas dan bawah sayap yang menghasilkan lift tersebut disebabkan oleh perbedaan kecepatan antara permukaan atas dan permukaan bawah sayap.

The Fall of the Theorem

Nah, sekarang, mari kita lihat kebenaran dari keempat claim yang diajukan oleh teori ini.

Claim pertama mengatakan bahwa agar pesawat dapat terbang (menghasilkan lift) panjang permukaan atas sayap lebih panjang daripada permukaan bawah sayap. Jikalau demikian, bagaimana dengan pesawat kertas? Bukankah pesawat kertas juga dapat menghasilkan lift? Kalau anda tidak yakin dengan masalah pesawat kertas, coba perhatikan dalam berbagai pertunjukan aerobatic udara, pesawat dapat terbang terbalik (upside-down) untuk durasi yang panjang. Kalau memang permukaan atas harus lebih panjang lintasannya, sekarang pesawat terbang dengan lintasan yang lebih panjang di bagian bawah, dan pesawatnya tidak jatuh!

Mari kita perhatikan juga pesawat ini. Pesawat ini adalah produksi Pitts Special, S-15.

Perhatikan penampang sayapnya, dapat dilihat bahwa sayap ini memiliki airfoil yang simetris terhadap garis tengah penampangnya. Artinya, aliran udara di bagian atas dan bagian bawah sayap menempuh panjang lintasan yang sama. Dan pesawat ini dapat terbang!

Teori ini walaupun kedengarannya benar, tetapi didasarkan pada asumsi yang salah, yaitu bahwa molekul udara harus bertemu lagi di ujung sayap sehingga aliran udara di bagian atas bergerak lebih cepat daripada udara di bagian bawah (claim No. 2). Memang benar bahwa aliran udara di bagian atas bergerak lebih cepat daripada udara di bagian bawah sayap. TETAPI, molekul yang tadinya bersebelahan dan kemudian berpisah ketika mengenai leading edge sayap TIDAK HARUS bertemu kembali dan kemudian bergerak bersama-sama lagi ketika meninggalkan trailing edge sayap. Artinya tidak ada yang salah dengan Hukum Bernoulli, hanya saja asumsi yang dipakai salah.

Bagian dari teori ini berusaha menghubungkan kecepatan aliran udara di bagian atas sayap dengan kecepatan di bagian bawah sayap dengan panjang lintasan bagian atas dan bawah sayap. Tetapi, hubungan/rumus ini didasarkan pada asumsi yang salah yaitu bahwa molekul udara harus bertemu kembali ketika meninggalkan trailing edge. Pada kenyataannya kecepatan aliran udara yang didapat dari hubungan ini tidak memberikan lift yang diukur dari wind tunnel test untuk suatuairfoil tertentu. Kecepatan di permukaan atas sayap jauh lebih cepat pada pengukuran wind tunnel test daripada yang diprediksikan oleh teori equal transit time ini.

Di artikel ini, kita akan coba menggunakan teori yang salah ini untuk mencoba menghitung secara kasar besarnya kecepatan yang diperlukan untuk terbang steady straight and level flight pada Cessna 172 dengan Maximum Take-off Weight di ketinggian permukaan air laut dan kondisi ISA.

DISCLAIMER: Pendekatan yang dilakukan di sini sifatnya sangat konservatif dan hanya dapat digunakan untuk memberikan semacam gambaran bagaimana teori ini gagal memprediksikan lift sebagaimana mestinya karena didasarkan pada asumsi yang salah.

Case Study: Cessna 172

Cessna 172 adalah salah satu pesawat latih yang sangat populer bahkan sampai saat ini. Pesawat ini memiliki spesifikasi sebagai berikut:

Length: 27 ft 2 in (8.28 m)

Wingspan: 36 ft 1 in (11.0 m)

Height: 8 ft 11 in (2.72 m)

Wing area: 174 ft² (16.2 m²)

Airfoil: NACA 2412 (modified)

Empty weight: 1,620 lb (736 kg)

Useful load: 830 lb (376 kg)

Max takeoff weight: 2,450 lb (1,113 kg)

Powerplant: 1× Lycoming IO-360-L2Aflat-4 engine, 160 hp (120 kW) at 2,400 rpm

Cruise Speed: 122 knots (140mph, 226 km/h)

Airfoil dari C172 adalah NACA 2412 seperti yang dapat dilihat di gambar di bawah ini. Penampang airfoil ini dibuat dengan menggunakan data dari Airfoil Database dari University of Illinois – Urbana Champaign. Dari koordinat dari database tersebut, kita dapat menghitung panjang lintasan di permukaan atas sayap dan panjang lintasan di permukaan bawah sayap dengan menggunakan program seperti MATLAB ataupun MS Excel. Misal kita sebut ratio/perbandingan antara panjang lintasan atas dan bawah tersebut adalah η:

Di mana SU dan SL menunjukkan luas permukaan di bagian atas dan bawah sayap.

Set-up dari persamaan Bernoulli untuk soal ini dapat digambarkan sebagai berikut. Freestream condition diasumsikan pada kondisi ISA permukaan laut. Kecepatan di freestream condition ini adalah cruise speed dari pesawat tersebut. Arah aliran udara di sini digambarkan seperti pada kondisi steady-straight-and-level flight. Besaran dengan subscript U menunjukkan besaran untuk bagian atas sayap, dan subscript L untuk bagian bawah sayap. Gaya L adalah lift yang dihasilkan oleh pesawat tersebut dan W adalah gaya berat (akibat gravitasi) dari pesawat.

Untuk kondisi steady-straight-and-level flight, gaya berat sama dengan lift yang dihasilkan oleh sayap pesawat.

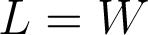
Kita bisa menulis 2 persamaan Bernoulli: 1. Dari freestream condition ke kondisi di permukaan atas sayap, dan 2. Dari freestream condition ke kondisi di permukaan bawah sayap. Persamaan tersebut adalah sebagai berikut:

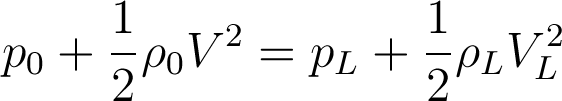
Selain itu, kita juga tau bahwa lift adalah akibat perbedaan tekanan antara permukaan atas dan permukaan bawah sayap. Secara matematis, kita dapat menulis persamaan berikut:

Atau

 Claim dari teori ini (yang salah) adalah kecepatan di atas dan bawah sayap dapat dihubungkan dengan persamaan:

Sehingga apabila kita selesaikan persamaan di atas kita bias dapatkan kecepatan di permukaan bawah sayap adalah:

Di mana

Sampai di sini kita akan melakukan beberapa pendekatan untuk memberikan suatu angka yang dapat kita interpretasikan. Pertama, kita asumsikan cruise speed pesawat (yaitu V0) dapat dilihat sebagai rata-rata dari kecepatan di atas dan di bawah permukaan sayap:

Selain itu, kita juga asumsikan bahwa SL mendekati luas permukaan sayap itu sendiri, S = 174 ft2 seperti diberikan oleh data C172 di atas.

Menghitung berapa kecepatan cruise speed C172 agar dapat terbang steady-straight-and-level dengan persamaan ini kita mendapat hasil 625 knots! Cruise speed ini 5 kali lebih besar daripada cruise speed normal C172. Dari sini dapat disimpulkan pula bahwa lift yang diprediksikan dengan menggunakan teori ini jauh lebih kecil daripada yang didapat pada kenyataannya1.

Jadi, bagaimana cara menghitung lift dari suatu airfoil?

Ada berbagai macam cara untuk menghitung lift (atau tepatnya koefisien dari lift). Satu cara ke cara yang lainnya menggunakan pendekatan yang berbeda dengan presisi masing-masing. Pendekatan yang paling sederhana adalah dengan menggunakan teorema Kutta-Joukowski untuk airfoil tipis. Pendekatan ini sering dikenal dengan sebutan “thin airfoil theory.” Prinsip teori ini adalah dengan meletakkan vortex source di sepanjang permukaan sayap. Dengan menyelesaikan persamaan syarat batas (boundary condition equation), lift dapat dihitung.

Pendekatan lain yang jauh lebih akurat daripada metode pertama ini adalah dengan melakukan simulasi yang melahirkan cabang ilmu Computational Fluid Dynamics (CFD). Simulasi ini dapat menghitung berbagai macam parameter aerodinamis dari suatu benda dalam aliran fluida. Lahirnya cabang ilmu ini didukung dengan semakin berkembangnya kemampuan komputer untuk melakukan komputasi. Cabang ilmu ini juga telah membuka suatu revolusi dari kemajuan ilmu aerodinamika sendiri. Sekarang, para aerodynamicists tidak perlu membuat prototype berulang kali untuk mendapatkan hasil yang mereka inginkan.

Tentu saja pada akhirnya yang dapat memberikan hasil paling akurat sesuai dengan kenyataan adalah wind tunnel testing. Untuk mengetahui lebih lanjut mengenai masalah ini, silahkan klik di sini.

Referensi:

1 NASA Glenn Research Center: http://www.grc.nasa.gov/WWW/K-12/airplane/wrong1.html

Source untuk Cessna 172 Specification adalah dari Wikipedia